Research


I am interested in algebraic topology and algebraic geometry. In particular much of my research has focused on the interplay between enumerative geometry and homotopy theory, particularly motivic and equivariant homotopy theory.

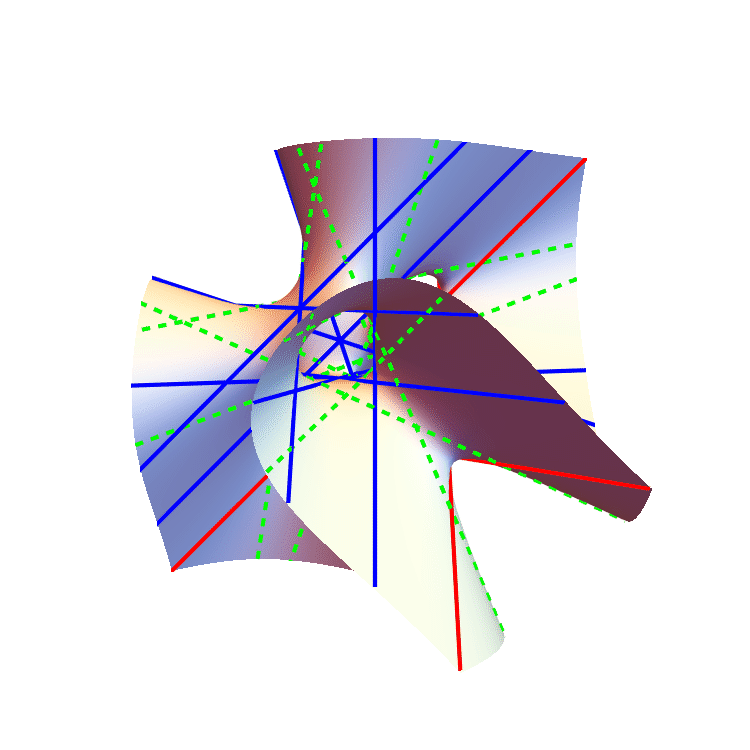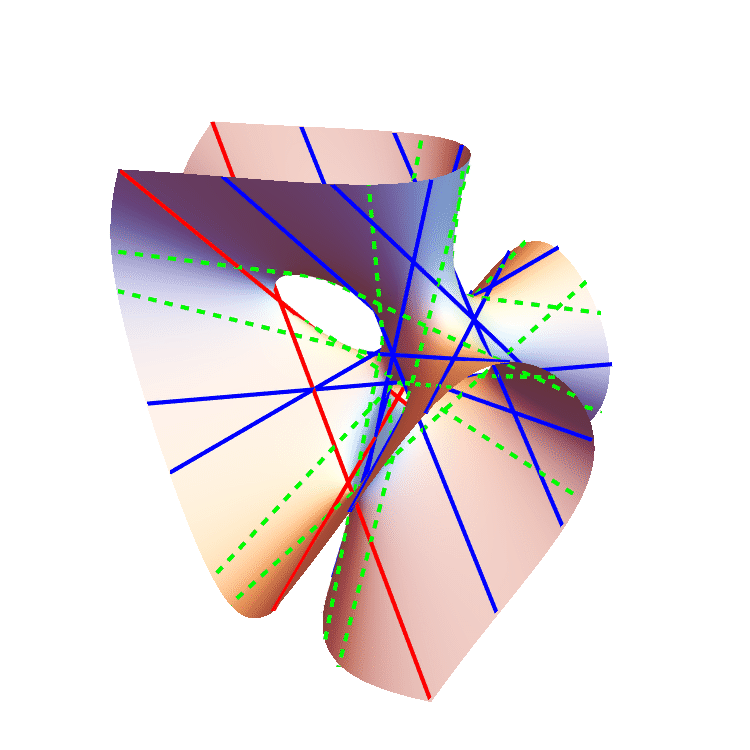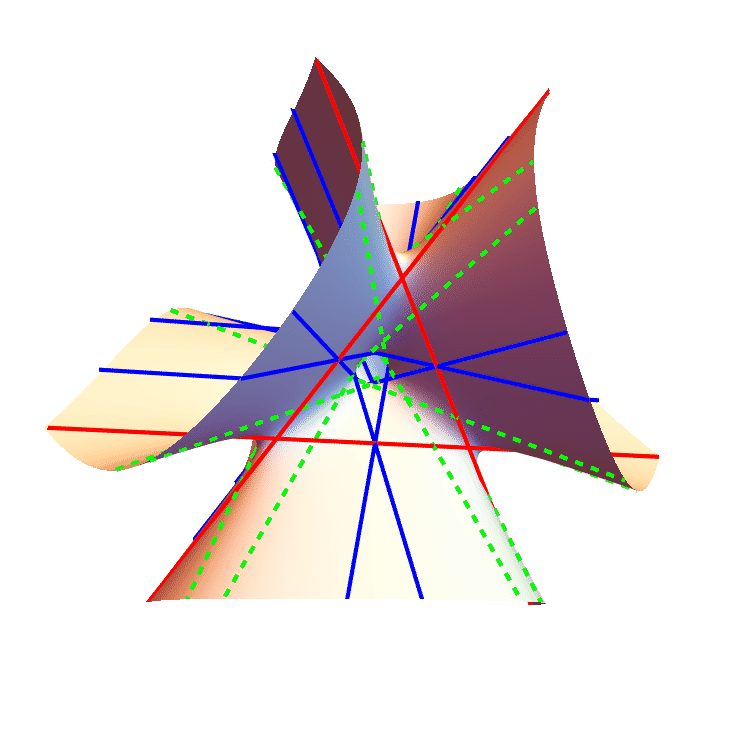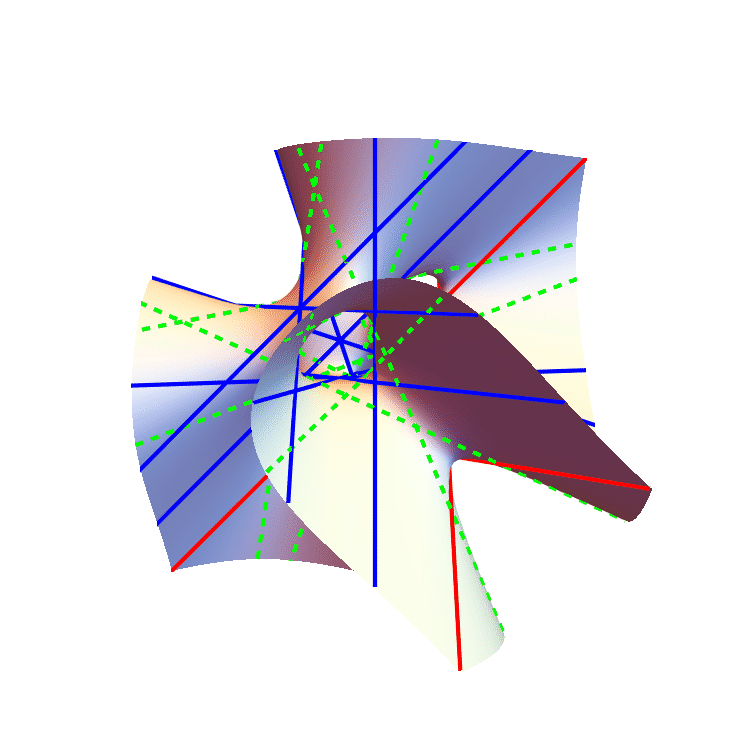
The $S_4$-orbits of the 27 lines on the Clebsch surface.

Papers and Preprints:

  1. $\mathbb{A}^1$-Brouwer degrees in Macaulay2, with N. Borisov, F. Espino, T. Hagedorn, Z. Han, J. Lopez Garcia, J. Louwsma, G. Ong, and A. Tawfeek.
    13 pages, 2023. Submitted.

    2. We describe the Macaulay2 package "A1BrouwerDegrees" for computing local and global $\mathbb{A}^1$-Brouwer degrees and studying symmetric bilinear forms over a field.

  2. Equivariant enumerative geometry,
    38 pages, 2023. Submitted.

    3. We formulate an equivariant conservation of number, which proves that a generalized Euler number of a complex equivariant vector bundle can be computed as a sum of local indices of an arbitrary section. This involves an expansion of the Pontryagin--Thom transfer in the equivariant setting. We leverage this result to commence a study of enumerative geometry in the presence of a group action. As an illustration of the power of this machinery, we prove that any smooth complex cubic surface defined by a symmetric polynomial has 27 lines whose orbit types under the $S_4$-action on $\mathbb{C}P^3$ are given by $[S_4/C_2]+[S_4/C_2'] + [S_4/D_8]$, where $C_2$ and $C_2'$ denote two non-conjugate cyclic subgroups of order two. As a consequence we demonstrate that a real symmetric cubic surface can only contain 3 or 27 lines.

  3. An enriched degree of the Wronski map,
    24 pages, 2023. Submitted.

    4. Given $mp$ different $p$-planes in general position in $(m+p)$-dimensional space, a classical problem is to ask how many $p$-planes intersect all of them. For example when $m=p=2$, this is precisely the question of "lines meeting four lines in 3-space" after projectivizing. The Brouwer degree of the Wronski map provides an answer to this general question, first computed by Schubert over the complex numbers and Eremenko and Gabrielov over the reals. We provide an enriched degree of the Wronski for all $m$ and $p$ even, valued in the Grothendieck--Witt ring of a field, using machinery from $\mathbb{A}^1$-homotopy theory. We further demonstrate in all parities that the local contribution of an $m$-plane is a determinantal relationship between certain Plücker coordinates of the $p$-planes it intersects.

  4. Residue sums of Dickson polynomials over finite fields, with J. Harrington, M. Litman, T.H.W. Wong,
    18 pages, 2021. Accepted pending revisions.

    5. Given a polynomial with integral coefficients, one can inquire about the possible residues it can take in its image modulo a prime $p$. The sum over the distinct residues can sometimes be computed independent of the prime $p$; for example, Gauss showed that the sum over quadratic residues vanishes modulo a prime. In this paper we provide a closed form for the sum over distinct residues in the image of Dickson polynomials of arbitrary degree over finite fields of odd characteristic, and prove a complete characterization of the size of the image set. Our result provides the first non-trivial classification of such a sum for a family of polynomials of unbounded degree.

  5. Lifts, transfers, and degrees of univariate maps, with S. McKean,
    Mathematica Scandinavica 129(1), 2023.

    6. One can compute the local $\mathbb{A}^1$-degree at points with separable residue field by base changing, working rationally, and post-composing with the field trace. We show that for endomorphisms of the affine line, one can compute the local $\mathbb{A}^1$-degree at points with inseparable residue field by taking a suitable lift of the polynomial and transferring its local degree. We also discuss the general set-up and strategy in terms of the six functor formalism. As an application, we show that trace forms of number fields are local $\mathbb{A}^1$-degrees.

  6. Bézoutians and the $\mathbb{A}^1$-degree, with S. McKean, S. Pauli,
    Algebra & Number Theory 17(11), 2023.

    7. We prove that both the local and global $\mathbb{A}^1$-degree of an endomorphism of affine space can be computed in terms of the multivariate Bézoutian. In particular, we show that the Bézoutian bilinear form, the Scheja-Storch form, and the $\mathbb{A}^1$-degree for complete intersections are isomorphic. Our global theorem generalizes Cazanave's theorem in the univariate case, and our local theorem generalizes Kass-Wickelgren's theorem on EKL forms and the local degree. This result provides an algebraic formula for local and global degrees in motivic homotopy theory.

  7. Homotopy Mackey functors of equivariant algebraic $K$-theory,
    Journal of Pure and Applied Algebra 226(8), 2022.

    8. Given a finite group $G$ acting on a ring $R$, Merling constructed an equivariant algebraic $K$-theory $G$-spectrum, and work of Malkiewich and Merling, as well as work of Barwick, provides an interpretation of this construction as a spectral Mackey functor. This construction is powerful, but highly categorical; as a result the Mackey functors comprising the homotopy are not obvious from the construction and have therefore not yet been calculated. In this work, we provide a computation of the homotopy Mackey functors of equivariant algebraic $K$-theory in terms of a purely algebraic construction. In particular, we construct Mackey functors out of the $n$th algebraic $K$-groups of group rings whose multiplication is twisted by the group action. Restrictions and transfers for these functors admit a tractable algebraic description in that they arise from restriction and extension of scalars along module categories of twisted group rings. In the case where the group action is trivial, our construction recovers work of Dress and Kuku from the 1980's which constructs Mackey functors out of the algebraic $K$-theory of group rings. We develop many families of examples of Mackey functors, both new and old, including $K$-theory of endomorphism rings, the $K$-theory of fixed subrings of Galois extensions, and (topological) Hochschild homology of twisted group rings.

  8. An introduction to $\mathbb{A}^1$-enumerative geometry,
    In Lecture Notes in Mathematics, vol 2292. Springer, 2021.

    9. We provide an expository introduction to $\mathbb{A}^1$-enumerative geometry, which uses the machinery of $\mathbb{A}^1$-homotopy theory to enrich classical enumerative geometry questions over a broader range of fields. Included is a discussion of enriched local degrees of morphisms of smooth schemes, following Morel, $\mathbb{A}^1$-Milnor numbers, as well as various computational tools and recent examples.

  9. A note on twisted group rings and semilinearization,
    Communications in Algebra, 49:8, 3380-3386, 2021.

    10. In this short note, we construct a right adjoint to the functor which associates to a ring $R$ equipped with a group action its twisted group ring. This right adjoint admits an interpretation as semilinearization, in that it sends an $R$-module to the group of semilinear $R$-module automorphisms of the module. As an immediate corollary, we provide a novel proof of the classical observation that modules over a twisted group ring are modules over the base ring together with a semilinear action.

  10. The trace of the local $\mathbb{A}^1$-degree, with R. Burklund, S. McKean, M. Montoro, M. Opie,
    Homology, Homotopy and Applications 23(1):243-255, 2021.

    11. We prove that the local $\mathbb{A}^1$-degree of a polynomial function at an isolated zero with finite separable residue field is given by the trace of the local $\mathbb{A}^1$-degree over the residue field. This fact was originally suggested by Morel's work on motivic transfers and by Kass and Wickelgren's work on the Scheja-Storch bilinear form. As a corollary, we generalize a result of Kass and Wickelgren's relating the Scheja-Storch form and the local $\mathbb{A}^1$-degree.

  11. Zeros of newform Eisenstein series on $\Gamma_0(N)$, with V. Jakicic,
    J. Number Theory (190):109-130, 2018.

    12. We examine the zeros of newform Eisenstein series $E_{\chi_1,\chi_2,k}(z)$ of weight $k$ on $\Gamma_0(q_1q_2)$, where $\chi_1$ and $\chi_2$ are primitive characters modulo $q_1$ and $q_2$, respectively. We determine the location and distribution of a significant fraction of the zeros of these Eisenstein series for $k$ sufficiently large.

  12. On consecutive $n$th roots of unity modulo $q$, with J. Harrington, S. Kannan, M. Litman,
    J. Number Theory (174):494-504, 2017.

    13. Given $n\in\mathbb{N}$, we study the conditions under which a finite field of prime order $q$ will have adjacent elements of multiplicative order $n$. In particular, we analyze the resultant of the cyclotomic polynomial $\Phi_n(x)$ with $\Phi_n(x+1)$, and exhibit Lucas and Mersenne divisors of this quantity. For each $n \ne 1,2,3,6$, we prove the existence of a prime $q_n$ for which there is an element $\alpha\in \mathbb{Z}/q_n$ where $\alpha$ and $\alpha+1$ both have multiplicative order $n$. Additionally, we use algebraic norms to set analytic upper bounds on the size and quantity of these primes. .

Software:

  • A1BrouwerDegrees.m2, a Macaulay2 package for computing local and global $\mathbb{A}^1$-Brouwer degrees, and manipulating the associated symmetric bilinear forms. With N. Borisov, F. Espino, T. Hagedorn, Z. Han, J. Lopez Garcia, J. Louwsma, G. Ong, and A. Tawfeek.

Other writing:

Notes:

Attached are expository sets of notes from various talks I've given. They are likely riddled with errors - please email me if you find any.

Conference and course notes:

Disclaimer: Any errors found in these notes should be attributed to me, not the original lecturer. If you find any typos or have suggestions, please feel free to contact me.