Symmetric quartics and bitangents
It is classical that a smooth plane quartic (in fact a general plane quartic) admits 28 bitangents, which are lines meeting the quartic at two points, each of order two. This is a classical question in enumerative algebraic geometry, and we can ask how it interacts with symmetries of quartics. Since a plane quartic is a canonical smooth curve of genus 3, its automorphism group lives in \(\text{PGL}_3(\mathbb{C})\) and therefore acts on the bitangents. There are 12 possible automorphism groups, and their action on the lines was worked out by me and Candace.
Listed below are the 12 automorphism groups, a picture of the real bitangents where available, and some info about how the group sits inside the Galois group of the problem, which is \(W(E_7)/\pm1\), or \(\text{PSL}(6,2)\) if you prefer.
| Type | Picture | Group name | GAP id | Normalizer id | Normalizer solvable? | Centralizer id | Centralizer solvable? | Normalizer mod group (id) | Normalizer mod group solvable? |
|---|---|---|---|---|---|---|---|---|---|
1 | 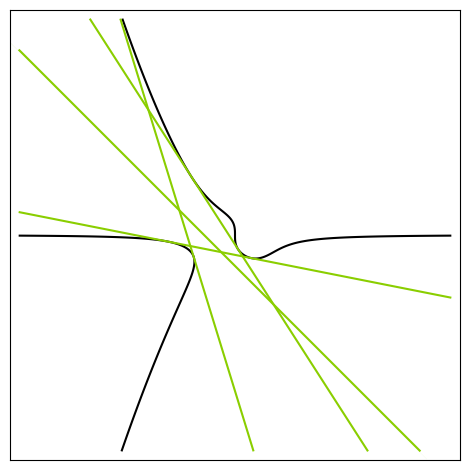 | \(\mathrm{PSL}_2(7)\) | [168, 42] | [336, 208] | false | [ 168, 42 ] | true | [2, 1] | true |
2 |  | \(C_4^{\times 2}\rtimes S_3\) | [96, 64] | [384, 17949] | true | [ 2, 1 ] | true | [4, 2] | true |
3 |  | \(C_4\circledcirc A_4\) | [48, 33] | [192, 988] | true | [ 48, 33 ] | true | [4, 2] | true |
4 | 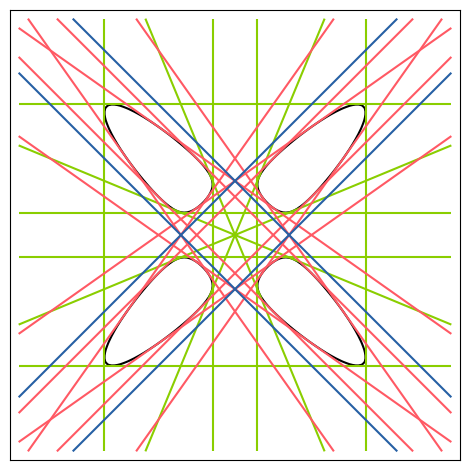 | \(S_4\) | [24, 12] | [96, 226] | true | [ 24, 12 ] | true | [4, 2] | true |
5 | 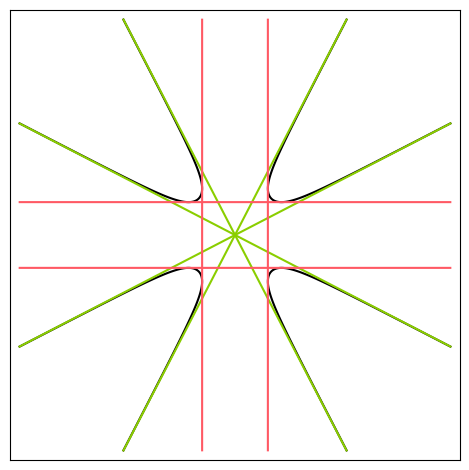 | \(P\) | [16, 13] | [768, 1090081] | true | [ 16, 13 ] | true | [48, 48] | true |
6 | 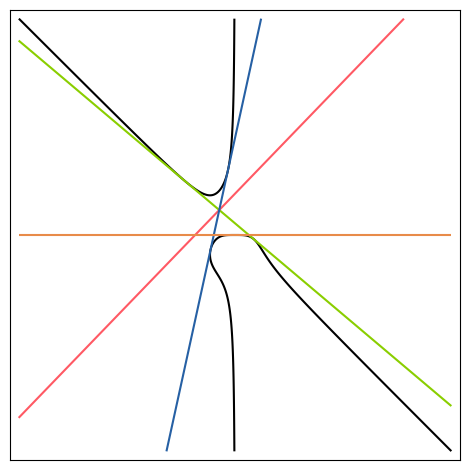 | \(C_9\) | [9, 1] | [54, 6] | true | [ 9, 1 ] | true | [6, 2] | true |
7 | 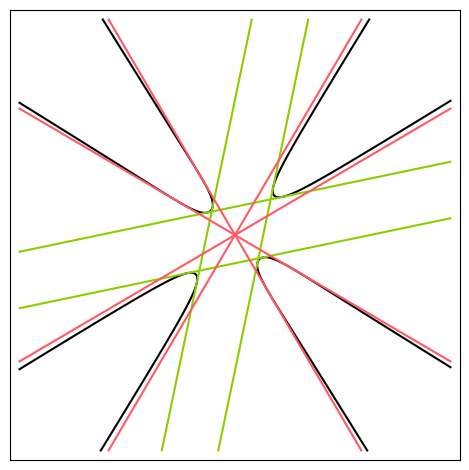 | \(D_8\) | [8, 3] | [256, 25876] | true | [ 8, 3 ] | true | [32, 27] | true |
8 | 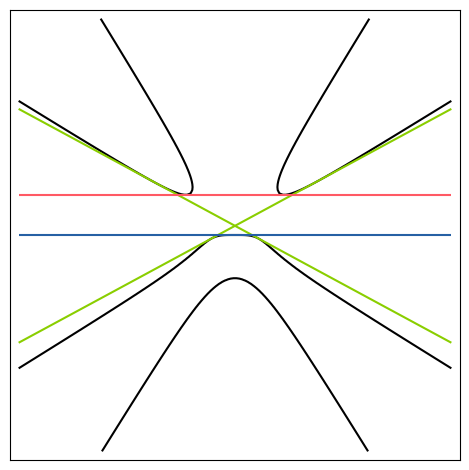 | \(C_6\) | [6, 2] | [144, 125] | true | [ 6, 2 ] | true | [24, 12] | true |
9 |  | \(S_3\) | [6, 1] | [216, 162] | true | [ 6, 1 ] | true | [36, 10] | true |
10 | 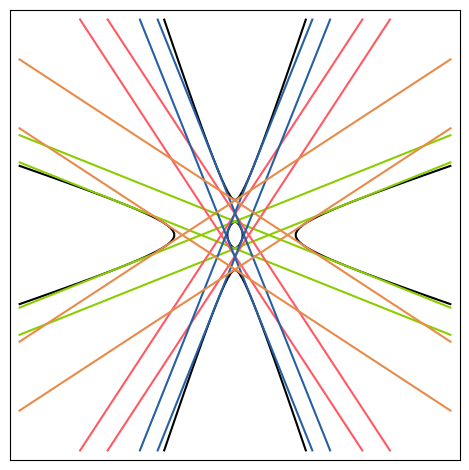 | \(K_4\) | [4, 2] | n/a (order 1536) | true | [ 4, 2 ] | true | [384, 20089] | true |
11 | 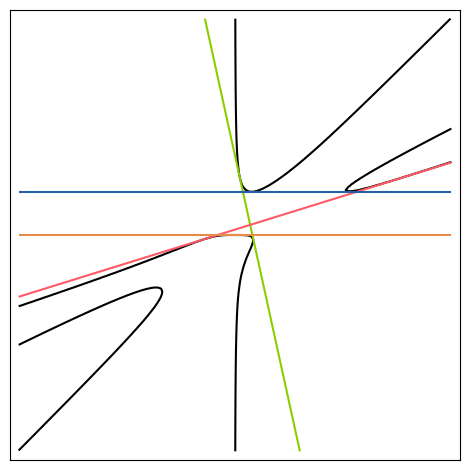 | \(C_3\) | [3, 1] | [1296, 2891] | true | [ 3, 1 ] | true | [432, 734] | true |
12 |  | \(C_2\) | [2, 1] | n/a (order 4608) | true | [ 2, 1 ] | true | n/a (order 2304) | true |
Subgroup lattice
Here is the subgroup lattice, where an edge indicates subconjugacy in \(\text{PGL}_3(\mathbb{C})\). I haven’t computed that this is the same as \(W(E_7)/\pm1\) subconjugacy in each of these cases.
On the Galois group
The Galois group of this problem is \(W(E_7)/\pm 1\). This is a finite group of order 1451520, and it is unsolvable.